Queue (data structure)

Representation of a FIFO Queue

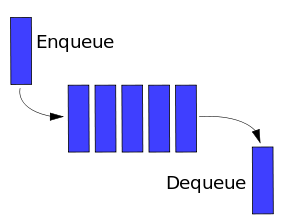
A queue (pronounced /kjuː/) is a particular kind of collection in which the entities in the collection are kept in order and the principal (or only) operations on the collection are the addition of entities to the rear terminal position and removal of entities from the front terminal position. This makes the queue a First-In-First-Out (FIFO) data structure. In a FIFO data structure, the first element added to the queue will be the first one to be removed. This is equivalent to the requirement that whenever an element is added, all elements that were added before have to be removed before the new element can be invoked. A queue is an example of a linear data structure.

Queues provide services in computer science, transport and operations research where various entities such as data, objects, persons, or events are stored and held to be processed later. In these contexts, the queue performs the function of a buffer.

Queues are common in computer programs, where they are implemented as data structures coupled with access routines, as an abstract data structure or in object-oriented languages as classes. Common implementations are circular buffers and linked lists.

Contents

Operations

Common operations from the C++ Standard Template Library include the following:

bool empty()
Returns True if the queue is empty, and False otherwise.
T& front()
Returns a reference to the value at the front of a non-empty queue. There is also a constant version of this function, const T& front().
void pop()
Removes the item at the front of a non-empty queue.
void push(const T& foo)
Inserts the argument foo at the back of the queue.
size_type size()
Returns the total number of elements in the queue.

Example C Program

#include <stdio.h>
 
int main(){
 
  int a[100],i,j;
 
  printf("To DQueue Enter -1\n");
 
  for(i=0;i<100;i++){
    printf("NQueue ");
 
      a[i]=0;
 
      if(i==0){
        printf("Wrong\n");
        continue;
      }
      printf("DQueue = %d\n",a[0]);
 
      for(j=0;j<i;j++)
        a[j]=a[j+1];
      i--;
    }
    else
      i++;
  }
 
  for(j=0;j<i;j++)
    printf("%d ",a[j]);
 
return 0;
}

Example Pascal Program

Based on an example in R.S Algorithms .

program queue;
 type
 link=^node;
 node=record 
 next:link;
 key:integer;
 end;
 
 var
 
 U:integer;
 tail,Head:link;
 
procedure queinit; // Initializes the queue
begin
 
	New(tail);
	tail^.next:=nil;
	head:=tail;
end;
 
procedure put(u: integer); // Puts number u into the queue
var
  t: link;
begin
  New(t);
  tail^.key := u;
  tail^.next := t;
  tail := t;
end;
 
 function pop:integer; //Pops one number at a time
 var
 s:link;
 begin
	pop:=head^.key;
	s:=head;
	head:=head^.next;
	dispose(s);
 end;
 
 function empty:boolean;//checks if the queue is empty
 begin
	empty:=head=tail;
 end;
 
begin
  queinit;
  u := 1; 
  put(u);  // Put 1 in the queue
 
  u := 2;
  put(u);  // Put 2 in the queue
 
  u := 3;
  put(u);  // Put 3 in the queue
end.

Example C# Class

using System;
 
namespace QueueExample
{
    public class Queue
    {
        private object[] _Queue;
        private int _HeadPointer;
        private int _TailPointer;
        private int _Size;
        private int _Count;
 
        #region Constructor
        public Queue(int Size)
        {
            this._Size = Size;
            this._Queue = new object[Size];
            this._HeadPointer = 0;
            this._TailPointer = 0;
            this._Count = 0;
        }
        #endregion
 
        #region Methods
        public virtual void Enqueue(object item)
        {
            lock (this)
            {
                if (this.IsFull())
                {
                    throw new Exception("Queue is full !");
                }
                else
                {
                    this._Queue[this._TailPointer] = item;
                    this._Count++;
                }
 
                // Bump tail pointer to next available location
                this._TailPointer = this._TailPointer + 1;
                if (this._TailPointer >= this._Queue.Length)
                {
                    this._TailPointer = 0;
                }
            }
        }
 
        public virtual object Dequeue()
        {
            lock (this)
            {
                object item = null;
 
                if (this.IsEmpty())
                {
                    throw new Exception("Queue is empty !");
                }
                else
                {
                    item = this._Queue[this._HeadPointer];
                    this._Count--;
 
                    // Bump head pointer, wrap to beginning if it reaches the end
                    this._HeadPointer = this._HeadPointer + 1;
                    if (this._HeadPointer >= this._Queue.Length)
                    {
                        this._HeadPointer = 0;
                    }
                }
 
                return item;
            }
        }
 
        public virtual bool IsEmpty()
        {
            return (this._Count == 0);
        }
 
        public virtual bool IsFull()
        {
            return (this._Count == this._Size);
        }
 
        public virtual int Count()
        {
            return this._Count;
        }
        #endregion
    }
}

Example Java Code

public void insert(Element x) {
        Node New;
        New = new Node(x, null);
        if (NodeHead == null) {
            NodeHead = New;
        } else {
            NodeEnd.Next = New;
        }
        NodeEnd = New;
    }
 
    public Element head() throws IllegalArgumentException {
        if (NodeHead == null) {
            throw new IllegalArgumentException();
        } else {
            return NodeHead.Info;
        }
    }
 
    public Queue() {
    // Return Empty Queue
        NodeHead = null;
        NodeEnd = null;
    }

Example Javascript Code

function Queue() {
    var data = [];
 
    this.isEmpty = function() {
        return (data.length == 0);
    };
 
    this.enqueue = function(obj) {
        data.push(obj);
    };
 
    this.dequeue = function() {
        return data.shift();
    };
 
    this.peek = function() {
        return data[0];
    };
 
    this.clear = function() {
        data = [];
    };
}

Representing a Queue

The defining attribute of a queue data structure is the fact that allows access to only the front and back of the structure. Furthermore, elements can only be removed from the front and can only be added to the back. In this way, an appropriate metaphor often used to represent queues is the idea of a checkout line (Ford/Topp p. 385). Other examples of queues are people traveling up an escalator, machine parts on an assembly line, or cars in line at a petrol station. The recurring theme is clear: queues are essentially the same as a queue you would get in a shop waiting to pay.

In each of the cases, the customer or object at the front of the line was the first one to enter, while at the end of the line is the last to have entered. Every time a customer finishes paying for their items (or a person steps off the escalator, or the machine part is removed from the assembly line, etc.) that object leaves the queue from the front. This represents the queue “dequeue” function. Every time another object or customer enters the line to wait, they join the end of the line and represent the “enqueue” function. The queue “size” function would return the length of the line, and the “empty” function would return true only if there was nothing in the line.

Queue implementation

Theoretically, one characteristic of a queue is that it does not have a specific capacity. Regardless of how many elements are already contained, a new element can always be added. It can also be empty, at which point removing an element will be impossible until a new element has been added again.

A practical implementation of a queue, e.g. with pointers, of course does have some capacity limit, that depends on the concrete situation it is used in. For a data structure the executing computer will eventually run out of memory, thus limiting the queue size. Queue overflow results from trying to add an element onto a full queue and queue underflow happens when trying to remove an element from an empty queue.

A bounded queue is a queue limited to a fixed number of items.

See also

References

External links

Data structures
Types
Collection · Container
Arrays
Associative array · Multimap · Set · Multiset · Hash table
Lists
Double-ended queue · Linked list · Queue · Stack · Circular Queue/Buffer  · Skip list
Trees
Graphs
Directed graph · Directed acyclic graph · Binary decision diagram
List of data structures

 This article incorporates public domain material from the NIST document "Bounded queue" by Paul E. Black (Dictionary of Algorithms and Data Structures).